Pierre de Fermat (1601 – 1665) was a French lawyer and mathematician who is credited with a number of early developments leading to the creation of infinitesimal calculus (a precursor to differential calculus). He also did extensive research into number theory, analytic geometry, probability and even optics. But the thing that he is most famous for is an unfinished theorem that became one of the most daunting mathematical puzzles of all time.
In 1637 while reading a copy of Arithmetica, an ancient Greek text on mathematics written by Diophantus, Fermat believed that he had come up with a solution to a problem that he had been working on for some time.
In highly simplified terms, he was working on a general case proof for a supposition based on an extension of the Pythagorean theorem. (In case you have forgotten, the Pythagorean theorem states that a^2 + b^2 = c^2, where a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse.)
Fermat had been playing around with different exponents applied to the Pythagorean theorem (a^n + b^n = c^n). He realized that there are no solutions in positive integers, if n is an integer greater than 2 (more specifically when n is an odd prime number equal to or greater than 3). While you can prove that there are no solutions for specific integers (Fermat himself provided a proof for the integer 4 and in subsequent years other mathematicians have offered proofs for other integers 3, 5, 7, and so on) there was no general case proof that could be applied to all integers.
But something in the text of Arithmetica inspired Fermat and in the margin of the book he scribbled a quick and somewhat enigmatic note that read:
It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain.
In the last thirty years of his life, Fermat never again wrote of his “truly marvelous proof” and nothing was ever published.
After his death in 1665 his son Clément-Samuel Fermat published a new edition of Arithmetica that included his father’s notes and that one cryptic note inspired scores of mathematicians to take up the challenge.
In 1816, and again in 1850, the French Academy of Sciences offered a prize for a general proof of Fermat’s Last Theorem and in 1908 a German industrialist Paul Wolfskehl offered 100,000 gold marks for anyone who could come up with a solution to the problem.
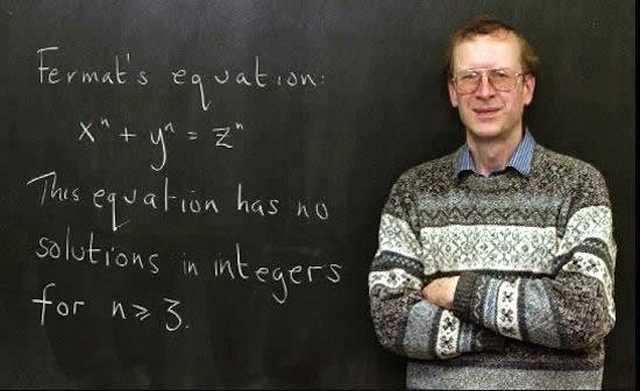
But it wasn’t until May 1995 that British mathematician Andrew Wiles (in collaboration with Richard Taylor and others) finally published two papers in the issue of the Annals of Mathematics providing a definitive general case proof. It had taken Wiles nearly eight years of his life (and a number of failures) to finally come up with a solution. (By the way, Wiles collected the Wolfskehl prize money, worth $50,000, on 27 June 1997.)
It’s interesting to note that in order to come up with his proof Wiles had to build upon on the works of many other modern mathematicians – works that would not have been available to Fermat at the time – so it’s highly unlikely that Fermat actually did come up with a “truly marvelous proof” of his own. But we’ll never know for sure.








